Über die Elementreihenfolge wird außerdem die Nummerierung der Gleichungen gesteuert. Damit hat sie auch Einfluss auf den Vorkonditionierer der implementierten iterativen Gleichungslöser (ILU = Incomplete LU Factorization).

Die Optimierung der Elementreihenfolge ("Reordering") erfolgt mit Rismo2D und hat zum Ziel, eine möglichst kurze Frontweite zu erreichen. Für einen Rismo2D-Lauf benötigen Sie die Geometriedatei:

• Steuerdatei (sample.ris)
• Querschnittsdatei (sample.sec)

Eine detaillierte Beschreibung der Eingabedateien finden Sie in den Kapiteln 6.1 bis 6.4. Im Folgenden werden kurz die zur Durchführung erforderlichen Einstellungen erläutert.

• Steuerdatei
  $RISMO2D 30900
  
  $SECTIONFILE         reorder.sec
  $REGIONFILE          sample-nr.inp
  
  $REPPORTFILE         reorder.out
  $GEO_UCDFILE         sample-rg.inp
  
  Angegeben sind hier nur die erforderlichen Dateien, von diesen beinhalten die rot eingefärbten Dateien relevante Informationen für das Reordering. In der Steuerdatei müssen nur die richtigen Dateinamen eingetragen werden. In der Datei $REGIONFILE steht das ungeordnete Finite Elemente Gitter, und in der Datei $GEO_UCDFILE finden Sie nach der Operation das geordnete Finite Elemente Gitter.
  Anmerkung: Die gewählten Endungen der Dateinamen (.ris|.sec|-nr.inp|...) sind willkürlich. Sie geben eine Namenskonvention wieder, die sich bei mir im Laufe der Zeit eingebürgert hat. Es steht Ihnen frei, diese Konvention zu übernehmen oder eine eigene zu verwenden.
  
  
• Zeitschritt-/Randbedingungsdatei
  $RISMO2D 30900
  
  $TM_CYCLE   95
  
  Mit diesen Einstellungen wird festgelegt, dass nur ein einziger Programmzyklus bearbeitet wird ($TM_CYCLE 95), in dem die Elementreihenfolge des FE-Gitters verbessert wird (Reordering). Der Algortihmus ist bei KING (1970) beschrieben.
  
  
• Querschnittsdatei
  $RISMO2D 30900
  
  # 2. Querschnitt   s +---------------------------------+ e
  #                    |                                 |
  # 1. Querschnitt   s +---------------------------------+ e
  
  #            xs       ys        xe       ye      Wsp
  $SECTION  193.723  283.844   193.133  285.640   99.00
  $SECTION  192.655  283.613   192.950  285.240   99.00
  $SECTION  191.676  284.624   192.937  285.423   99.00
  $SECTION  191.344  285.179   193.527  286.399   99.00
  $SECTION  191.351  285.227   192.117  287.715   99.00
  $SECTION  191.256  285.179   190.917  286.948   99.00
  $SECTION  190.612  284.800   189.927  286.880   99.00
  $SECTION  189.572  284.386   189.101  286.148   99.00
  $SECTION  187.813  284.173   189.067  286.047   99.00
  $SECTION  187.372  285.545   188.992  286.114   99.00
  
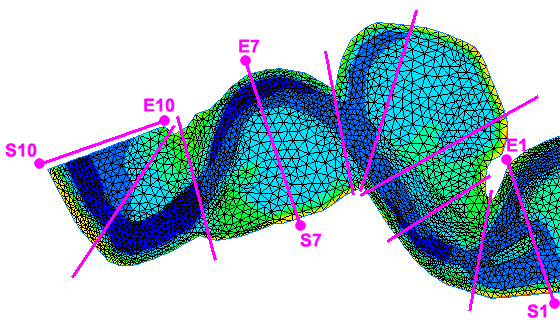
  Die Optimierung der Elementreihenfolge erfolgt mit einem rekursiven Algorithmus. Die Bestimmung der optimalen Reihenfolge würde für größere Finite-Elemente-Gitter einen imensen Rechenaufwand erfordern. Daher ist es erforderlich den Algorithmus mit der Vorgabe einiger "Ordnungsprofile" zu unterstützen. Diese Profile werden üblicherweise wie in Bild 1 dargestellt angeordnet. Die Vorgabe der Profileckpunkte in der Querschnittsdatei erfordert die strikte Einhaltung der dort definierten Reihenfolge und Orientierung.
  

Bild 1: Querprofile für das Reordering

Der Fortschritt des Reorderings wird kontinuierlich auf dem Bildschrim ausgegeben. Eine Zusammenfassung der Erzielten maximalen und mittleren Frontweite finden Sie in der Reportdatei:

(MODEL::ReorderElem) front width of corner nodes
                     maximum: 56
                     average: 37.49

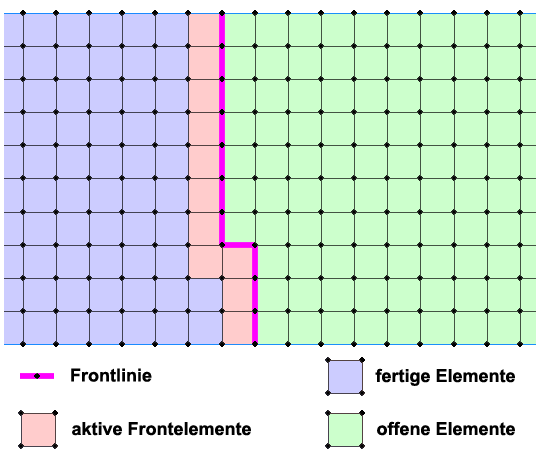
Die maximale Frontweite (hier: mfc = 56) gibt an, wieviele Eckknoten des Gitters während der elementweisen Lösung des Gleichungssystems maximal offen bleiben (Bild 2). Abhängig vom Typ der Differentialgleichung lässt sich hieraus die maximale Zahl der offenen Gleichungen abschätzen. Es gilt z.B.:

• Strömungsberechnung (quadratische Interpolation)   $TM_CYCLE 1, 2, 3:
  3 Gleichung je Eckknoten und 2 Gleichung je Kante:
  mfw ≥ mfc·3 + (mfc-1)·2    (z.Zt das Maximum)
  
  
• k-ε-Modell (quadratische Interpolation)   $TM_CYCLE 81, 82, 83:
  2 Gleichung je Eckknoten und 2 Gleichung je Kante:
  mfw ≥ mfc·2 + (mfc-1)·2
  
  
• Stofftransport (quadratische Interpolation)   $TM_CYCLE 50:
  1 Gleichung je Eckknoten und 1 Gleichung je Kante:
  mfw ≥ mfc·1 + (mfc-1)·1

Bild 2: Frontverlauf im Berechnungsgitter