6.1 Beschreibung der Steuerungsdatei
Mit der Version 3.09.00 liegen die Eingabedateien
- sample.ris // 6.1 Steuerungsdatei
- sample.tm // 6.2 Randbedingungs-/Zeitschrittdatei
- sample.tbl // 6.3 Materialdatei
- sample.sec // 6.4 Querschnittsdatei
in einem neuen völlig freien Format vor. Das alte Dateiformat kann zwar weiterhin eingelesen werden, aktuelle und künftige Neuerungen stehen dann allerdings nicht zur Verfügung. Rismo2D unterscheidet die neuen von den alten Eingabedateien durch ein Schlüsselwort in der 1. Zeile:
$RISMO2D 30900
Jede weitere Zeile mit relevanten Programmparametern beginnt ebenfalls mit einem Schlüsselwort. Alle anderen Zeilen werden überlesen und können daher beliebige Kommentare enthalten. Auch Zeilen, die mit einem Kommentarzeichen # oder * in der ersten Spalte beginnen, bleiben unberücksichtigt. Dies bietet die Möglichkeit, Zeilen mit Schlüsselworten vorübergehend zu deaktivieren.
Die Schlüsselworte können in einer beliebigen Reihenfolge eingegeben werden. Außerdem können die Schlüsselworte fehlen, die für einen Programmlauf nicht benötigt werden, oder bei denen Sie Standardwerte verwenden möchten.
6.2 Beschreibung der Zeitschritt-/Randbedingungsdatei
Für einen Zeitschritt können Sie einerseits Randbedingungen vorgeben und andererseits die zu bearbeitenden Programmzyklen ($TM_CYCLE). Ein Programmzyklus kann z.B. die Lösung der Flachwassergleichung oder die Lösung der k-e-Gleichungen sein.
Fehlt das Schlüsselwort $TIMESTEPFILE in der Steuerdatei, versucht Rismo2D die im Folgenden definierten Schlüsselworte aus der Steuerdatei einzulesen:
alphabetische Liste
| $TM_BOUND_LINE | $TM_BOUND_NODE | $TM_CYCLE | $TM_INTERVAL |
| $TM_MAXITER | $TM_OUTPUT | $TM_SOLVER | $TM_STEP_NO |
| $TM_STEPS | $TM_TURBULENCE | $TM_WEIGHT |
|
Die Zeitschrittwichtung J gilt (z.Zt.) gleichermaßen für alle Differentialgleichungen. Der Standardwert entspricht dem Zentraldifferenzenverfahren: $TM_WEIGHT 0.5 Für J sind allgemein Werte zulässig im Bereich von 0,0 < J ≤ 1,0. Dabei entspricht:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Für die Lösung stationärer Gleichungen spielen diese Parameter keine Rolle. Für eine instationäre Simulation legen Sie hier mit dem Parameter <timeInterval> die Zeitdiskretisierung fest (vgl. $TM_CYCLE 2 und 5). Die Länge des Zeitintervalls hat einen entscheidenden Einfluss auf das Verhalten der Strömung. Wenn Sie beispielsweise instationäre Prozesse, wie z.B. die Kármánsche Wirbelstraße, nachbilden möchten, ist neben einer ausreichenden räumlichen auch eine ausreichende zeitliche Auflösung der Strömung erforderlich. Auch bei einer instationären Simulation sind in jedem Zeitschritt mehrere Iterationen bis zur Konvergenz erforderlich. Der Zeitgradient wird im Rahmen dieser Iterationen iterativ bestimmt. Aus diesem Grund ist die Zeitschrittlänge unabhängig vom so genannten Courant-Kriterium und kann frei gewählt werden. Der zur Zeit übliche Lösungsweg zur Berechnung stationärer Strömungen beruht ebenfalls auf den instationären Gleichungen, die nun jedoch in einer vereinfachten Form gelöst werden; auf die iterative Bestimmung der Zeitgradienten wird verzichtet (vgl. $TM_CYCLE 3 und 6). Im Gegensatz zur instationären Simulation wird hierzu ein sehr langer quasi stationärer Zeitschritt gewählt (z.B. 1 Tag = 86.400 Sekunden). Es empfiehlt sich jedoch die Simulation mit einem sehr kurzen "relaxierten Zeitschritt" zu beginnen, um die Iterationen zu stabilisieren (vgl. auch den $RELAX-Parameter in der Steuerdatei). Ein Anhaltswert für die Wahl des relaxierten Zeitschritts ist das Courant-Kriterium (Courant-Zahl Cu):
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
$TM_OUTPUT <no1>,<no2>,... $TM_OUTPUT <fst> to <lst> step <inc> Mit diesem Parameter legen Sie fest zu welchen Zeitschritten eine Ausgabe der Berechnungsergebnisse erfolgen soll. Die Vorgabe der Zeitschritte kann in zwei verschiedenen Formaten erfolgen. Entweder durch eine mit Komma oder Leerzeichen separierte Liste: $TM_OUTPUT 5,10,15,20,25,30,35,40,45,50 oder durch einen Ausdruck ählich dem Schleifenbefehl in der Programmiersprache Basic: $TM_OUTPUT 5 to 50 step 5 Beide Zeilen bewirken eine Ausgabe zu den gleichen Zeitschritten. Falls der Parameter nicht angegeben wird, erfolgt eine Ausgabe zu jedem Zeitschritt. Nach dem letzten Zeitschritt erfolgt immer eine Ausgabe.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Zeitschrittsteuerung
$TM_STEPS <first> <last> <loop> Hier definieren Sie mit den Parametern <first> und <last> die Anzahl der Zeitschritte, die in dem Berechnungslauf abgearbeitet werden sollen. Es müssen nicht für jeden zu berechnenden Zeitschritt Randbedingungen vorgegeben werden. Sobald der letzte Zeitschritt mit Vorgaben bearbeitet wurde, verwendet Rismo2D den im Parameter <loop> definierten Zeitschritt und wiederholt ab diesem Zeitschritt die Abfolge der Rabdbedingungen. Der Zweck des Parameters <loop> kann einerseits zur Definition von periodischen Randbedingungen verwendet werden, und andererseits, um z.B. Stofftransport- und Strömungsberechnung in einer definierten Abfolge von Zeitschritten durchzuführen. Folgendes Beispiel soll die Zeitschrittsteuerung veranschaulichen:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
$TM_STEP_NO <no> Der Parameter $TM_STEP_NO leitet einen neuen Block mit Parametern (Programmzyklen und Randbedingungen) für den Zeitschritt <no> ein. Falls dieser Parameter fehlt, werden alle Parameter dem Zeitschritt 1 zugeordnet.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Steuerung des Programmablaufs im Zeitschritt $TM_CYCLE <cycle_1> <cycle_2> ... $TM_TURBULENCE <turb_1> <turb_2> ... $TM_MAXITER <maxiter_1> <maxiter_2> ... Mit diesen Parametern steuern Sie den Programmablauf in einem Zeitschritt. Aus der unten gegebenen tabellarischen Liste wählen Sie zum einen eine Folge von Programmzyklen ($TM_CYCLE), das heißt eine Abfolge von Gleichungen, die in dem Zeitschritt gelöst werden sollen. Für die stationäre Strömungsberechung eines Flusses mit einem algebraischen Turbulenzmodell wählen Sie zum Beispiel: $TM_CYCLE 90 60 3 Für jeden Programmzyklus definieren Sie außerdem ein Turbulenzmodell <turb>, die maximale Anzahl der Iterationen <maxiter> sowie einen Gleichungslöser <solver> aus der Definitionsliste in der Steuerdatei (vgl. $SOLVER). Das Turbulenzmodell hat nur Einfluss auf die Berechnung im Strömungsmodell sowie im k-e-Modell. Sie wäjhlen das Turbulenzmodell mit einer dreistelligen Zahl. Folgende Wahlmöglichkeiten stehen Ihnen zur Verfügung:
Der vollständige Programmablaufsteuerung für die stationäre Strömungsberechung eines Flusses mit dem algebraischen ELDER-Turbulenzmodell würde folgende Eingabe erfordern: $TM_CYCLE 90 60 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Randbedingungen an Knoten
$TM_BOUND_NODE <no> <type> <U> <V> <S> <K> <D> <C> Mit diesem Parameter legen Sie Randbedingungen für den Knoten <no> fest. Die Interpretation der Parameter <U> <V> <S> <K> <D> <C> hängt von <type> ab. Eine Übersicht der für Knoten definierbaren Randbedingungen gibt die folgende Tabelle.
Die Buchstaben D = Dirchlet-Randbedingung, N = Neumann-Randbedingung und C = Cauchy-Randbedingung geben den Typ der Randbedingung an. Die einzelnen Randbedingungen können im Rahmen des physikalisch/numerisch Sinnvollen durch eine einfache Addition des Parameters <type> überlagert werden. (Die Nummern sind jeweils 2er-Potenzen, so dass keine Seiteneffekte auftreten können.) Beispiel: Sollen an einem Auslaufrandknoten (Typ 2) eine Strömungsrichtung (Typ 4) und die Turbulenzparameter k und e (Typ 32) vorgegeben werden, so lautet der Randbedingungstyp: type = 2 + 4 + 32 = 38.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
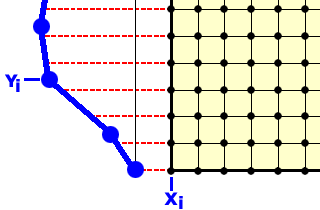
$TM_BOUND_LINE <no> <type> <X> <Y> <U> <V> <S> <K> <D> <C> Dieser Parameter ist eine Erweiterung des Parameters $TM_BOUND_NODE und soll die Vorgabe von Randbedingungen vereinfachen. Wenn Sie mehrere Zeilen mit Koordinaten <X> <Y> vorgeben. werden die vorgegebenen Randbedingungen auf die Knoten der Kontrolllinie interpoliert, wie dies die folgende Abbildung veranschaulicht:
Neben den bereits für Knoten definierten Randbedingungen können auf Kontrolllinien weitere Typen von Randbedingungen definiert werden. Mit <no> wird die Nummer einer Kontrolllinie angegeben. Die Randbedingung gilt für alle Knoten dieser Kontrolllinie. Die Interpretation der Parameter <X> <Y> <U> <V> <S> <K> <D> <C> hängt von <type> ab.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
letzte Änderung:
|